How Do You Know if a Function Is Exponential Growth or Decay

Learning Outcomes

• Graph exponential growth and decay functions.
• Solve problems involving radioactive decay, carbon dating, and half life.

Exponential Growth and Decay

In real-world applications, nosotros demand to model the behavior of a office. In mathematical modeling, nosotros choose a familiar general office with properties that suggest that information technology will model the real-world phenomenon we wish to clarify. In the case of rapid growth, we may choose the exponential growth role:

[latex]y={A}_{0}{e}^{kt}[/latex]

where [latex]{A}_{0}[/latex] is equal to the value at time goose egg, eastward is Euler's abiding, and k is a positive constant that determines the rate (percent) of growth. We may use the exponential growth function in applications involving doubling time, the time information technology takes for a quantity to double. Such phenomena as wildlife populations, financial investments, biological samples, and natural resources may exhibit growth based on a doubling time. In some applications, withal, as we will see when we discuss the logistic equation, the logistic model sometimes fits the information better than the exponential model.

On the other hand, if a quantity is falling rapidly toward zero, without always reaching cypher, then we should probably choose the exponential disuse model. Once more, we have the grade [latex]y={A}_{0}{east}^{-kt}[/latex] where [latex]{A}_{0}[/latex] is the starting value, and e is Euler'southward abiding. At present k is a negative constant that determines the rate of decay. We may utilize the exponential disuse model when nosotros are calculating half-life, or the time it takes for a substance to exponentially decay to one-half of its original quantity. We use half-life in applications involving radioactive isotopes.

In our choice of a part to serve every bit a mathematical model, nosotros often use information points gathered by careful observation and measurement to construct points on a graph and hope we tin can recognize the shape of the graph. Exponential growth and disuse graphs have a distinctive shape, equally we can see in the graphs below. Information technology is important to remember that, although parts of each of the ii graphs seem to lie on the x-centrality, they are really a tiny altitude in a higher place the ten-centrality.

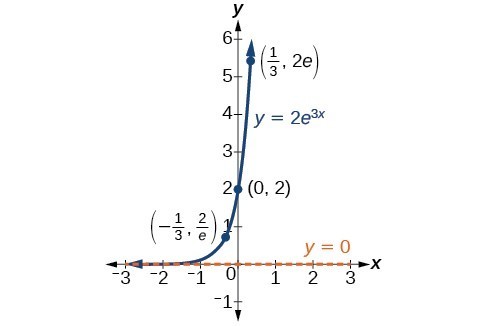
A graph showing exponential growth. The equation is [latex]y=2{east}^{3x}[/latex].

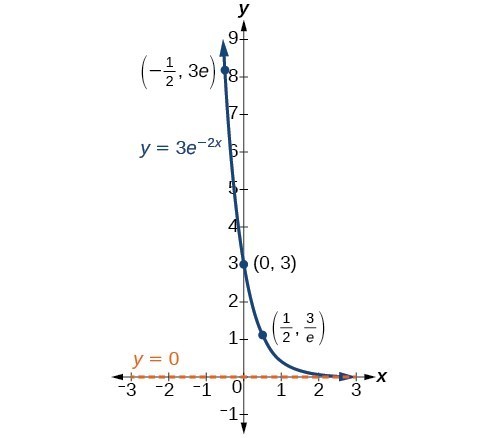
A graph showing exponential disuse. The equation is [latex]y=3{e}^{-2x}[/latex].

Exponential growth and disuse ofttimes involve very big or very modest numbers. To describe these numbers, we often apply orders of magnitude. The order of magnitude is the power of ten when the number is expressed in scientific note with i digit to the left of the decimal. For example, the altitude to the nearest star, Proxima Centauri, measured in kilometers, is 40,113,497,200,000 kilometers. Expressed in scientific annotation, this is [latex]4.01134972\times {10}^{xiii}[/latex]. We could describe this number as having order of magnitude [latex]{10}^{13}[/latex].

A General Annotation: Characteristics of the Exponential Function [latex]y=A_{0}e^{kt}[/latex]

An exponential part of the course [latex]y={A}_{0}{eastward}^{kt}[/latex] has the following characteristics:

• one-to-ane office
• horizontal asymptote: y= 0
• domain: [latex]\left(-\infty , \infty \right)[/latex]
• range: [latex]\left(0,\infty \right)[/latex]
• x intercept: none
• y-intercept: [latex]\left(0,{A}_{0}\correct)[/latex]
• increasing if m> 0
• decreasing if k< 0

An exponential part models exponential growth when chiliad > 0 and exponential decay when k < 0.

Example: Graphing Exponential Growth

A population of bacteria doubles every hour. If the culture started with 10 bacteria, graph the population as a function of time.

Calculating Doubling Fourth dimension

For growing quantities, we might want to discover out how long it takes for a quantity to double. As we mentioned to a higher place, the time information technology takes for a quantity to double is called the doubling time.

Given the basic exponential growth equation [latex]A={A}_{0}{eastward}^{kt}[/latex], doubling fourth dimension can be found by solving for when the original quantity has doubled, that is, by solving [latex]2{A}_{0}={A}_{0}{eastward}^{kt}[/latex].

The formula is derived as follows:

[latex]\brainstorm{array}{l}2{A}_{0}={A}_{0}{eastward}^{kt}\hfill & \hfill \\ 2={due east}^{kt}\hfill & \text{Divide both sides past }{A}_{0}.\hfill \\ \mathrm{ln}2=kt\hfill & \text{Accept the natural logarithm of both sides}.\hfill \\ t=\frac{\mathrm{ln}2}{k}\hfill & \text{Divide by the coefficient of }t.\hfill \terminate{array}[/latex]

Thus the doubling fourth dimension is

[latex]t=\frac{\mathrm{ln}2}{thou}[/latex]

Example: Finding a Part That Describes Exponential Growth

According to Moore'south Law, the doubling time for the number of transistors that tin be put on a computer chip is approximately ii years. Give a part that describes this behavior.

Try It

Recent information suggests that, as of 2013, the charge per unit of growth predicted past Moore's Law no longer holds. Growth has slowed to a doubling time of approximately three years. Discover the new function that takes that longer doubling time into account.

Show Solution

[latex]f\left(t\right)={A}_{0}{e}^{\frac{\mathrm{ln}2}{iii}t}[/latex]

Half-Life

Nosotros now plow to exponential disuse. I of the common terms associated with exponential disuse, equally stated above, is half-life, the length of time it takes an exponentially decaying quantity to decrease to half its original amount. Every radioactive isotope has a half-life, and the process describing the exponential decay of an isotope is called radioactive decay.

To observe the one-half-life of a function describing exponential disuse, solve the following equation:

[latex]\frac{1}{2}{A}_{0}={A}_{o}{e}^{kt}[/latex]

We find that the half-life depends just on the constant one thousand and not on the starting quantity [latex]{A}_{0}[/latex].

The formula is derived as follows

[latex]\begin{array}{l}\frac{1}{2}{A}_{0}={A}_{o}{eastward}^{kt}\hfill & \hfill \\ \frac{one}{2}={e}^{kt}\hfill & \text{Divide both sides by }{A}_{0}.\hfill \\ \mathrm{ln}\left(\frac{one}{2}\correct)=kt\hfill & \text{Take the natural log of both sides}.\hfill \\ -\mathrm{ln}\left(2\right)=kt\hfill & \text{Employ properties of logarithms}.\hfill \\ -\frac{\mathrm{ln}\left(2\right)}{k}=t\hfill & \text{Dissever by }yard.\hfill \finish{array}[/latex]

Since t, the time, is positive, k must, as expected, be negative. This gives us the half-life formula

[latex]t=-\frac{\mathrm{ln}\left(2\right)}{k}[/latex]

In previous sections, we learned the backdrop and rules for both exponential and logarithmic functions. Nosotros have seen that any exponential function tin be written equally a logarithmic function and vice versa. Nosotros take used exponents to solve logarithmic equations and logarithms to solve exponential equations. We are now ready to combine our skills to solve equations that model existent-world situations, whether the unknown is in an exponent or in the statement of a logarithm.

One such awarding is in science, in calculating the time information technology takes for half of the unstable material in a sample of a radioactive substance to disuse, called its half-life. The table beneath lists the half-life for several of the more than common radioactive substances.

Substance	Apply	Half-life
gallium-67	nuclear medicine	fourscore hours
cobalt-threescore	manufacturing	5.3 years
technetium-99m	nuclear medicine	6 hours
americium-241	structure	432 years
carbon-14	archeological dating	five,715 years
uranium-235	diminutive power	703,800,000 years

We can run into how widely the half-lives for these substances vary. Knowing the half-life of a substance allows us to calculate the amount remaining after a specified time. Nosotros can use the formula for radioactive decay:

[latex]\begin{assortment}{l}A\left(t\right)={A}_{0}{eastward}^{\frac{\mathrm{ln}\left(0.5\correct)}{T}t}\hfill \\ A\left(t\right)={A}_{0}{due east}^{\mathrm{ln}\left(0.5\right)\frac{t}{T}}\hfill \\ A\left(t\right)={A}_{0}{\left({e}^{\mathrm{ln}\left(0.5\right)}\right)}^{\frac{t}{T}}\hfill \\ A\left(t\right)={A}_{0}{\left(\frac{ane}{ii}\right)}^{\frac{t}{T}}\hfill \stop{array}[/latex]

where

• [latex]{A}_{0}[/latex] is the amount initially present
• [latex]T[/latex] is the half-life of the substance
• [latex]t[/latex] is the time flow over which the substance is studied
• [latex]A[/latex], or [latex]A(t)[/latex], is the amount of the substance present afterwards time [latex]t[/latex]

How To: Given the one-half-life, find the decay rate

1. Write [latex]A={A}_{o}{e}^{kt}[/latex].
2. Replace A past [latex]\frac{1}{2}{A}_{0}[/latex] and supervene upon t by the given half-life.
3. Solve to notice thousand. Express m every bit an exact value (do non round).

Annotation: It is also possible to detect the disuse charge per unit using [latex]k=-\frac{\mathrm{ln}\left(2\right)}{t}[/latex].

Example: Using the Formula for Radioactive Disuse to Find the Quantity of a Substance

How long will information technology take for 10% of a chiliad-gram sample of uranium-235 to disuse?

Endeavour It

How long will information technology take before twenty percent of our 1000-gram sample of uranium-235 has decayed?

Show Solution

[latex]t=703,800,000\times \frac{\mathrm{ln}\left(0.8\right)}{\mathrm{ln}\left(0.5\right)}\text{ years }\approx \text{ }226,572,993\text{ years}[/latex].

Example: Finding the Function that Describes Radioactive Disuse

The one-half-life of carbon-14 is v,730 years. Express the amount of carbon-fourteen remaining as a function of time, t.

Try It

The half-life of plutonium-244 is lxxx,000,000 years. Find a function that gives the corporeality of plutonium-244 remaining as a function of time measured in years.

Show Solution

[latex]f\left(t\right)={A}_{0}{e}^{-0.0000000087t}[/latex]

Radiocarbon Dating

The formula for radioactive decay is important in radiocarbon datingwhich is used to calculate the estimate appointment a establish or creature died. Radiocarbon dating was discovered in 1949 by Willard Libby who won a Nobel Prize for his discovery. Information technology compares the difference between the ratio of ii isotopes of carbon in an organic antiquity or fossil to the ratio of those two isotopes in the air. It is believed to exist accurate to inside about 1% error for plants or animals that died within the final 60,000 years.

Carbon-fourteen is a radioactive isotope of carbon that has a one-half-life of five,730 years. It occurs in pocket-sized quantities in the carbon dioxide in the air we breathe. Well-nigh of the carbon on Earth is carbon-12 which has an diminutive weight of 12 and is not radioactive. Scientists accept determined the ratio of carbon-14 to carbon-12 in the air for the final lx,000 years using tree rings and other organic samples of known dates—although the ratio has changed slightly over the centuries.

As long equally a plant or animal is alive, the ratio of the two isotopes of carbon in its body is shut to the ratio in the temper. When it dies, the carbon-14 in its torso decays and is not replaced. By comparing the ratio of carbon-14 to carbon-12 in a decaying sample to the known ratio in the atmosphere, the date the plant or animate being died can be approximated.

Since the half-life of carbon-14 is 5,730 years, the formula for the amount of carbon-fourteen remaining later t years is

[latex]A\approx {A}_{0}{e}^{\left(\frac{\mathrm{ln}\left(0.five\right)}{5730}\right)t}[/latex]

where

• [latex]A[/latex] is the corporeality of carbon-14 remaining
• [latex]{A}_{0}[/latex] is the corporeality of carbon-14 when the plant or fauna began decaying.

This formula is derived equally follows:

[latex]\begin{array}{50}\text{ }A={A}_{0}{eastward}^{kt}\hfill & \text{The continuous growth formula}.\hfill \\ \text{ }0.five{A}_{0}={A}_{0}{e}^{k\cdot 5730}\hfill & \text{Substitute the half-life for }t\text{ and }0.5{A}_{0}\text{ for }f\left(t\correct).\hfill \\ \text{ }0.5={east}^{5730k}\hfill & \text{Divide both sides past }{A}_{0}.\hfill \\ \mathrm{ln}\left(0.5\correct)=5730k\hfill & \text{Take the natural log of both sides}.\hfill \\ \text{ }g=\frac{\mathrm{ln}\left(0.5\right)}{5730}\hfill & \text{Split up both sides by the coefficient of }1000.\hfill \\ \text{ }A={A}_{0}{east}^{\left(\frac{\mathrm{ln}\left(0.v\right)}{5730}\right)t}\hfill & \text{Substitute for }r\text{ in the continuous growth formula}.\hfill \end{array}[/latex]

To find the age of an object we solve this equation for t:

[latex]t=\frac{\mathrm{ln}\left(\frac{A}{{A}_{0}}\correct)}{-0.000121}[/latex]

Out of necessity, nosotros fail hither the many details that a scientist takes into consideration when doing carbon-fourteen dating, and we just look at the basic formula. The ratio of carbon-xiv to carbon-12 in the atmosphere is approximately 0.0000000001%. Permit r be the ratio of carbon-14 to carbon-12 in the organic antiquity or fossil to be dated determined by a method called liquid scintillation. From the equation [latex]A\approx {A}_{0}{e}^{-0.000121t}[/latex] we know the ratio of the pct of carbon-14 in the object we are dating to the percentage of carbon-14 in the temper is [latex]r=\frac{A}{{A}_{0}}\approx {e}^{-0.000121t}[/latex]. We solve this equation for t, to get

[latex]t=\frac{\mathrm{ln}\left(r\right)}{-0.000121}[/latex]

How To: Given the percentage of carbon-14 in an object, make up one's mind its age

1. Express the given per centum of carbon-14 every bit an equivalent decimal r.
2. Substitute for rin the equation [latex]t=\frac{\mathrm{ln}\left(r\right)}{-0.000121}[/latex] and solve for the historic period, t.

Case: Finding the Historic period of a Bone

A bone fragment is found that contains 20% of its original carbon-14. To the nearest year, how quondam is the bone?

Effort It

Cesium-137 has a half-life of nearly 30 years. If nosotros begin with 200 mg of cesium-137, volition it take more or less than 230 years until only 1 milligram remains?

Prove Solution

less than 230 years; 229.3157 to be exact

Contribute!

Did you have an idea for improving this content? We'd love your input.

Improve this pageLearn More

mooreseesculde1951.blogspot.com

Source: https://courses.lumenlearning.com/waymakercollegealgebra/chapter/exponential-growth-and-decay/